Add initial LOBPCG top-k eigenvalue solver (#3112) #10962
Conversation
|
Thanks for your pull request! It looks like this may be your first contribution to a Google open source project. Before we can look at your pull request, you'll need to sign a Contributor License Agreement (CLA). View this failed invocation of the CLA check for more information. For the most up to date status, view the checks section at the bottom of the pull request. |
vlad17
force-pushed
the
topk
branch
3 times, most recently
from
3d3cfc5 to
18b1d8e
Compare
vlad17
force-pushed
the
topk
branch
2 times, most recently
from
21173cc to
9e0ed50
Compare
tests/lobpcg_test.py
Outdated
| 'jax_traceback_filtering': 'off', | ||
| } | ||
|
|
||
| # TODO(vladf): add f64 tests just to verify it compiles? |
There was a problem hiding this comment.
I think that would be good -- you could probably check if it's running on CPU and disable otherwise?
There was a problem hiding this comment.
It looks like there are f64 tests auto-triggered by the github action matrix (via env var), so I think all I should really need to do here is adjust the epsilons.
|
A couple high level thoughts:
Neither of these are deal breakers for the first iteration, though. |
Great idea, this should be easy to add and now that I think about it, and I think Shankar (skrishnan@google.com) was another user who'd immediately benefit from an interface like that.
Could you elaborate on this? I'd be very willing to do this as a follow-on if I had a user to work with on their ideal API for this, but as-stated I don't quite see how setting the initial |
Wouldn't we want to calculate the matrix P from the previous iteration? |
|
Ah, gotcha. I guess that makes sense, and it seems like it'd be a matter of exposing the |
|
Here are some cool curves (which can be generated from the tests) of jax vs scipy f32 on 1000x1000 versions of the test matrices for top-10 eigs (I set convergence tol to 0 which is why nothing converges)
|
I would like to reproduce these tests in SciPy standalone and check if some bugs need to be fixed there, since the runs appear too unstable. Could you please upload the code that calls SciPy for these tests? Which version of SciPy have you used to get these plots? |
|
@lobpcg I used 1.8.0 (did anything change in 1.8.1?). The examples are all the same as the unit tests in the PR but size 1000. The actual colab to make the viz depends on some Google-internal features for unrelated things, but I can try to find some time to clean up the notebook for a public-facing version. Would it be more appropriate to post that as a scipy github issue? Just to keep this thread focussed on jax. |
1.8.0 is representative. I made changes in lobpcg specifically for float32, but that was before. Of course if you create the reproducible issue in SciPy that would be ideal. No need to include the code to make the actual plots, just please add a reference to your post with the plots above and a ping to me. If SciPy fails on smaller sizes like 100, all those would be good examples to include into SciPy as unit tests, if I find a fix so that they all run. |
|
@lobpcg filled out scipy/scipy#16408 with just the cases, no viz. |
jax/experimental/sparse/linalg.py
Outdated
| - Despite increased iteration cost, we always maintain an orthonormal basis | ||
| for the block search directions. | ||
| - We change the convergence criterion; see the `tol` argument. | ||
| - Soft locking is intentionally not implemented; it relies on choosing an |
There was a problem hiding this comment.
Maybe refer to a paper where soft locking is introduced here?
There was a problem hiding this comment.
There isn't a canonical link (a very long researchgate URL is all I could find since the original host is gone). So I left a DOI.
There was a problem hiding this comment.
In particular, the following link is the original source I believe, but broken:
http://math.cudenver.edu/%CB%9Caknyazev/research/conf/cm04%20soft%20locking/cm04.pdf
Research gate has a not-so-pretty URL but works:
https://www.researchgate.net/publication/343530965_Hard_and_soft_locking_Hard_and_soft_locking_in_iterative_methods_for_symmetric_eigenvalue_problems
Perhaps @lobpcg might have a better reference for this?
jax/experimental/sparse/linalg.py
Outdated
| action. | ||
| X : An `(n, k)` array representing the initial search directions for the `k` | ||
| desired top eigenvectors. This need not be orthogonal, but must be | ||
| linearly independent. |
There was a problem hiding this comment.
"linearly independent" is not a very precise term in finite precision. I assume the method gradually breaks down as cond(X) increases?
There was a problem hiding this comment.
Yeah, I orthonormalize it upon entry, so technically it's "linearly independent enough, such that the orthogonalization routine does not decide it's rank-deficient according to its cutoffs". I'll try to phrase that concisely.
| subspace of) the Krylov basis `{X, A X, A^2 X, ..., A^m X}`. | ||
| tol : A float convergence tolerance; an eigenpair `(lambda, v)` is converged | ||
| when its residual L2 norm `r = |A v - lambda v|` is below | ||
| `tol * 10 * n * (lambda + |A v|)`, which |
There was a problem hiding this comment.
The factor n is probably quite conservative. Using a probabilistic argument it might be worth trying to scale as sqrt(n) instead. But there might be counter examples.
There was a problem hiding this comment.
Discussed offline: n just happened to work best for making the tolerances on the unit test all be around floating point epsilon (and scipy usually uses this factor for eigenvalue routines)
| return w[::-1], V[:, ::-1] | ||
|
|
||
|
|
||
| def _svqb(X): |
There was a problem hiding this comment.
Please add a docstring for this method, it is quite non-trivial. Please write out the math instead of just giving a reference.
jax/experimental/sparse/linalg.py
Outdated
|
|
||
|
|
||
| def _project_out(basis, U): | ||
| # "twice is enough" from shoyer's reference: |
jax/experimental/sparse/linalg.py
Outdated
| # | ||
| # Usually it requires solving the complicated standard eigensystem | ||
| # U^-T S^T A S U^-1 @ Q = w * Q and then backsolving V = U^-1 Q, | ||
| # but if S is standard orthonormal then we just need to find |
There was a problem hiding this comment.
I think this comment is probably more confusing than helpful. Maybe just mention that we keep S orthonormal, in which case we just need to solve the projected eigenvalue problem for S.T@A@S to obtain the Ritz values and vectors of A w.r.t . span(S).
| # | ||
| # https://epubs.siam.org/doi/abs/10.1137/0725014 | ||
| # https://www.jstage.jst.go.jp/article/ipsjdc/2/0/2_0_298/_article | ||
| n, k = X.shape |
There was a problem hiding this comment.
Please write out the math here instead of just citing the papers. The code is not particularly readable with all the concatenations etc.
| """Derives a truncated orthonormal basis for `X`. | ||
| SVQB [1] is an accelerator-friendly orthonormalization procedure, which | ||
| squares the matrix `C = X.T @ X` and computes an eigenbasis for a smaller |
There was a problem hiding this comment.
I think you could use QR instead of an eigendecomposition if X is full rank, and even Cholesky if X is sufficiently well-conditioned. Both these options would be more accelerator-friendly.
See, e.g.: https://epubs.siam.org/doi/abs/10.1137/18M1218212
However, I don't that you can know that these are safe to use. But it's worth thinking about as it might allow you to work with larger k.
There was a problem hiding this comment.
Rank revealing QR would be a nice option, if it was available in JAX. It might be worth adding. A version based on the randomized projection approach could be made accelerator-friendly.
There was a problem hiding this comment.
By QR here, you mean QR-ing X itself not its square right? At one point early in the algorithm development process I tried that but decided against it b/c the speed wasn't satisfactory. Cholesky on XTX would be faster but rank deficiency is specifically a case that needs to be handled here.
That said, I'll put trying the QR approach out again on my TODO list. It's worth revisiting and I don't have hard numbers saying it's too slow. And it avoids squaring.
I'm really intrigued by the randomized projection you're mentioning. Do you have a reference?
There was a problem hiding this comment.
Here is a reference for the RRQR with randomized projection: https://arxiv.org/abs/2008.04447
You are right that computing the QR decomposition of X is likely slower, since X.T@X is so fast on an accelerator. But avoiding the squaring would be nice. Just some things to experiment with, I guess.
| are mutually orthonormal. | ||
| """ | ||
|
|
||
| # See Sec. 6.9 of The Symmetric Eigenvalue Problem by Beresford Parlett [1] |
google-ml-butler
bot
added
kokoro:force-run
pull ready
vlad17
force-pushed
the
topk
branch
2 times, most recently
from
b7c5016 to
4bf25e5
Compare
This initial version is f32-only for accelerators, since it relies on an eigh call (which itself is f32 at most) in its inner loop. For details, see jax.experimental.linalg.standard_lobpcg documentation. This is a partial implementation of the similar [scipy lobpcg function](https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.linalg.lobpcg.html).
6 participants
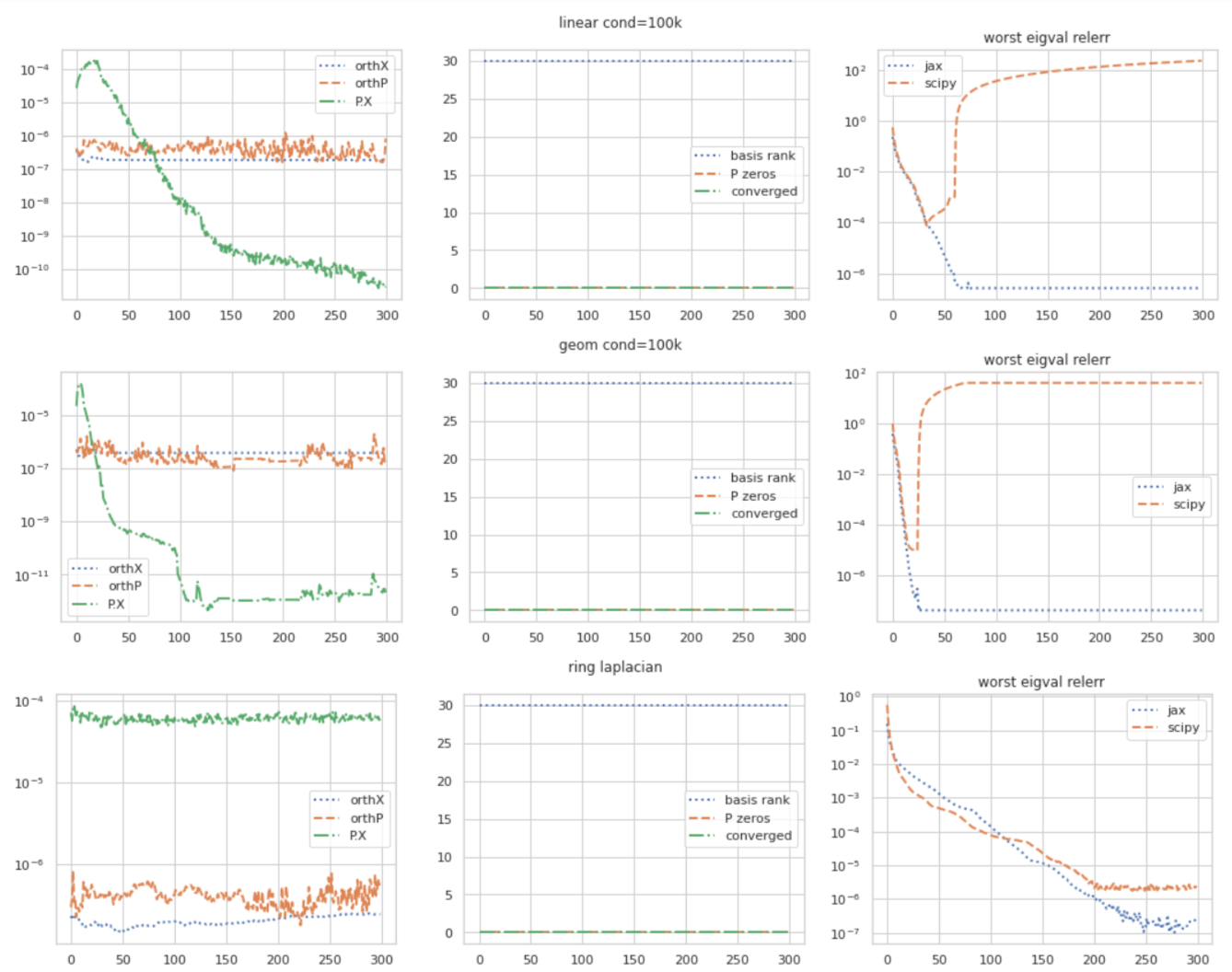
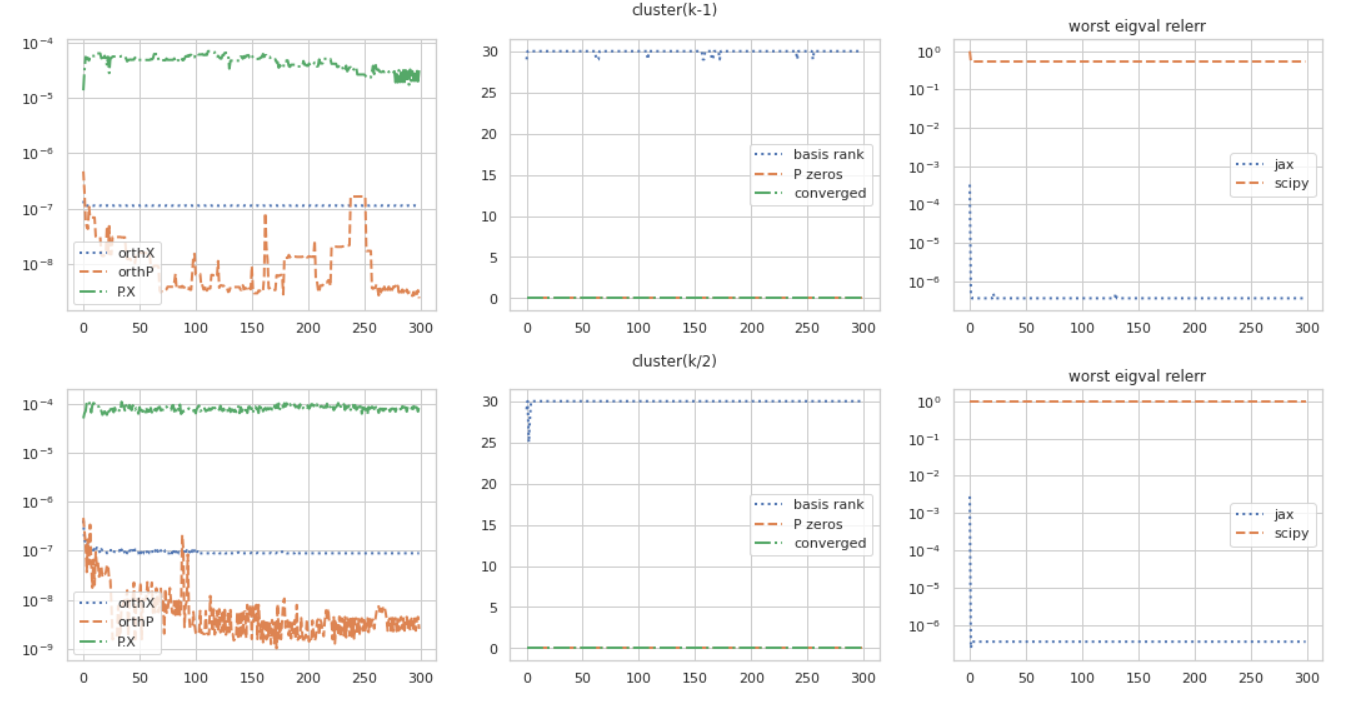
This initial version is f32-only for accelerators, since it relies on an eigh call (which itself is f32 at most) in its inner loop.
For details, see jax.experimental.linalg.standard_lobpcg documentation.