Kumpulan Soal dan Pembahasan Materi Refleksi Pencerminan Transformasi Geometri

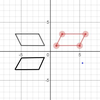
KOMPAS.com - Refleksi atau pencerminan adalah suatu transformasi yang memindahkan tiap titik pada bidang dengan menggunakan sifat bayangan cermin.

Dilansir dari buku Matematika Kelompok Sosial, Administrasi Perkantoran, dan Akuntansi (2008) oleh Muhamad Yusup, pencerminan dinotasikan dengan a adalah sumbu cermin.

Sifat-sifat pencerminan adalah:

• Jarak dari titik asal ke cermin sama dengan jarak cermin ke titik bayangan
• Garis yang menghubungkan titik asal dengan titik bayangan tegak lurus terhadap cermin

Adapun pemetaan dan matriks yang bersesuaian dengan pencerminan di atas dapat dirangkum sebagai berikut:

Baca juga: Konsep dan Contoh Soal Transformasi pada Refleksi (Pencerminan)

Pencerminan	Pemetaan	Matriks
Pencerminan terhadap sumbu-x	Mx: P(x,y) → P'(x,-y)
Pencerminan terhadap sumbu-y	My: P(x,y) → P'(-x,y)
Pencerminan terhadap garis y = x	My-x: P(x,y) → P'(y,x)
Pencerminan terhadap garis y = -x	My=-x: P(x,y) → P'(-y,-x)
Pencerminan terhadap titik asal O (0,0)	Mo: P(x,y) → P'(-x,-y)

Baca juga: Pencerminan (Refleksi) dalam Geometri

Contoh soal 1

Tentukan bayangan dari setiap titik pada pencerminan titik (3,-5) oleh pencerminan terhadap sumbu-x.

Jawab:

Dengan menggunakan perkalian matriks, x' dan y' ditentukan sebagai berikut:

Jadi, bayangan titik P(3,-5) oleh pencerminan terhadap sumbu-x adalah titik P'(3,5).

Baca juga: Refleksi Jajargenjang, Jawaban Soal TVRI 12 Mei 2020

Contoh soal 2

Tentukan bayangan dari setiap titik pada pencerminan titik (-1,-3) oleh pencerminan terhadap garis y = x.

Jawab:

Dengan menggunakan perkalian matriks, x' dan y' ditentukan sebagai berikut:

Jadi, bayangan titik P(-1,-3) oleh pencerminan terhadap garis y = x adalah titik P'(-3, -1).

Baca juga: Pengertian dan Gambar dari Pencerminan, Perputaran, dan Kesebangunan Bangun Datar

Contoh soal 3

Tentukan bayangan dari setiap titik pada pencerminan titik (5,2) oleh pencerminan terhadap titik asal O (0,0).

Jawab:

Dengan menggunakan perkalian matriks, x' dan y' ditentukan sebagai berikut:

Jadi, bayangan titik P (5,2) oleh pencerminanatau refleksi terhadap titik asal O (0,0) adalah titik P(-5,-2).

Baca juga: Konsep dan Contoh Soal Transformasi pada Refleksi (Pencerminan)

Contoh soal 4

Tentukan bayangan persamaan garis x-2y-3=0 oleh pencerminan terhadap sumbu-x.

Jawab:

dengan x' = x ⇔ x = x'
y' = -y ⇔ y = -y'

Dengan mensubstitusikan x'=x dan y'=-y pada persamaan garis x-2y-3=0 diperoleh:

x-2y-3=0
(x')-2(-y')-3=0
x'+2y'-3=0

Jadi, bayangan persamaan garis x-2y-3=0 oleh pencerminan terhadap sumbu x adalah x+2y-3=0.

Itulah penjelasan mengenai pengertian refleksi atau pencerminan transformasi geometri beserta contoh soal dan pembahasannya.

Baca juga: Pencerminan (Refleksi) dalam Geometri